활성화 함수

 

 

 

 

 

글을 작성하는 데에 아래 자료를 참고하였습니다.

• 블로그 글
• 딥러닝의 정석 (한빛미디어)

 

1. 활성화 함수 사용 이유¶

 

• 선형 뉴런
  • 선형으로 이루어진 $z$에 적용 되는 함수 $f$
  • $f(x) = az + b$
  • 계산하기는 쉽지만 은닉층이 없는 신경망으로 표현될 수 있음
  • 은닉층이 없다면 복잡한 관계를 학습하기 어렵다는 문제가 있다

 

• 활성화 함수는 딥러닝에 비선형성을 도입하기 위한 방법이다.

 

• 바람직한 활성화 함수
  • Gradient Vanishing 문제가 없어야한다
    • 활성화 함수는 결과값이 0~1사이 값이라면, 역전파 과정에서 여러번 곱해지다보면 초기 학습되던 값이 소실되는 문제가 생겨 학습이 재대로 되지 않을 수 있다.
  • Zero-Centered
    • 활성화 함수의 출력은 기울기가 특정 방향으로 이동하지 않도록 0에서 대칭이어야 합니다.
  • 계산 비용
    • 활성화 함수는 모든 계층 후에 적용되며 심층 네트워크에서 수백만 번 계산해야 하기 때문에 계산비용이 작아야 한다.
  • 미분 가능
    • 언급한 바와 같이 신경망은 경사 하강법을 사용하여 훈련되므로 모델의 레이어는 부분적으로 미분 가능하거나 최소한 미분 가능해야 한다.

 

2. Step function¶

 

$$H[n] = \begin{cases} 0, \;n<0\\ 1, \;n\geq0 \end{cases}$$

 

 

• 설명
  • 0 이상일 때 1 0보다 작을 때는 0을 출력한다.
  • 공학에서는 이 함수는 ON OFF로 사용 된다.

 

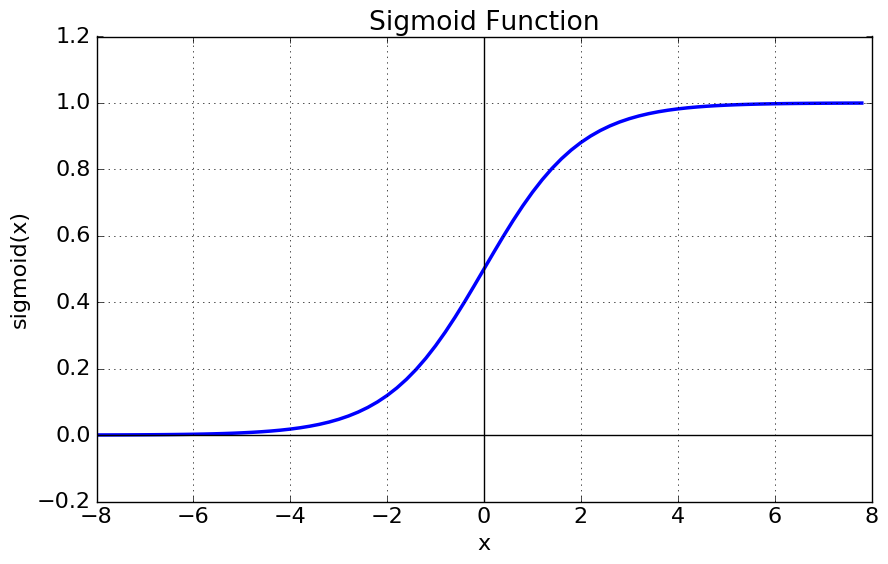
3. Sigmoid function¶

 

$$f(z) = \frac{1}{(1+e)^{-z}}$$

 

 

 

• 설명
  • s자 형태로 이루어진 이 함수는 0 ~ 1 사이의 값을 가진다. 즉 아무리 절대값이 커져도 결과값은 커지지 않는다.
  • Step function의 큰 단점은 미분을 할 수 없다는 문제가 있는데 sigmoid 함수는 이를 해결할 수 있다.
• 단점
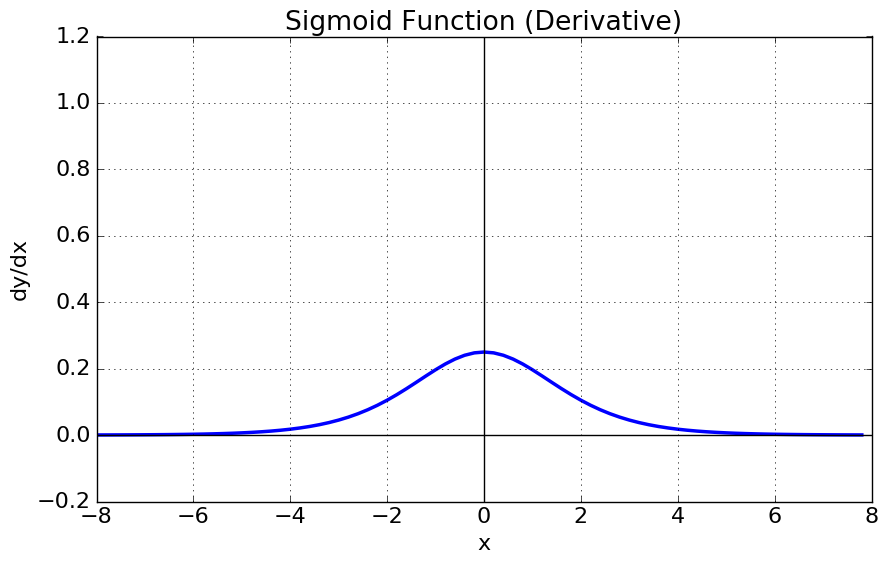
  • Gradient Vanishing 현상
    • sigmoid 함수를 미분하게 되면 최대값이 1보다 작으며, 절대값이 커질수록 0에 가까워진다. 즉 x값이 커질수록 미분을 하게되면 값이 없어지는 문제가 생긴다.
  • 함수값의 중심이 0이 아니다. 이는 학습의 속도를 느리게 만들 수 있다.
  • 지수함수를 사용하기 때문에 컴퓨터의 계산 비용이 크다

 

4. tanh function¶

 

 

$$f(z) = tanh(z)$$

 

• 설명
  • tanh 함수는 0이 중심이기 때문에 sigmoid 함수보다 선호되는 경우가 많다.
  • 다중 클래스 분류 문제 에 사용
  • 0 ~ 1 사이의 값을 가지기 때문에 모델의 최종 계층으로 상용된다

 

5. Lelu 함수¶

 

$$f(z) = max(0, z)$$

 

 

• 장점
  • 계산하기 쉽다.
  • Gradient Vanishing 문제를 발생시키지 않는다.
• 단점
  • 모든 음수 출력에 대해 0이기 때문에 일부 노드가 아무것도 학습하지 못하게 된다.
  • 한계값이 inf 이기 때문에 값이 너무 커질 가능성이 있다.

 

6. Leaky ReLU function¶

 

$$f(z) = max(ax, x)$$

 

 

• 설명
  • $a$는 일반적으로 0.01 로 설정되는 하이퍼파라미터
  • LeLU 함수가 음수일 때 학습을 제대로 못하는 단점 극복하기 위해 사용

 

7. ReLU6¶

 

$$f(z) = min(max(0,x),6)$$

 

 

• 값이 극단적으로 커지는 문제점을 해결하기 위해 사용

In [3]:

 

 

 

In [ ]: